고객들이 이 제품을 살 것이냐 안 살것이냐와 같이 ‘Yes or No’ 2개의 선택지의 확률을 구할 때 사용하는 것이 로지스틱 회귀(Logistic Regression)이다. 예를 들어 다음의 마케팅 문제들이 있다.
- 소비를 할 것인가? (아니면 저축을 할 것인가?)
- 브랜드 A를 선택할 것인가? (아니면 다른 브랜드를 선택할 것인가?)
- 이메일 마케팅에 응답을 할 것인가?
이렇게 예, 아니오로 답변이 가능한 변수를 이항 변수(binomial variable)라고 하고, 로지스틱 회귀에서 종속 변수인 y값은 당연히 이산적(discrete)이다.
■ 로지스틱 회귀는 언제 사용하나요?
만약 아래와 같은 선형 회귀식이 있다고 하자.
y_n = w_0 + w_nx_n+ ε_n
yn은 n명의 고객의 최종 선택이다. 예를 들어 yn = 1일 경우에 브랜드 A를 선택하고, 0일 경우에 다른 브랜드를 선택함을 보여준다. w0은 임의의 절편값이고, wn 역시 임의의 기울기 값이다(w는 가중치(weight)에서 따왔다.). xn 은 브랜드를 선택할 때 영향을 미치는 요인들을 뜻한다. 예를 들어 가격, 맛, 색상 등등으로 기업에서 관찰할 수 있는 요소다. 마지막으로 εn 은 오차값인데 기업에서 관측할 수 없는 소비자 개개인의 특성, 소비자가 선택을 할 때 매장의 분위기 등등을 모두 포함한다.
선형 모델은 기본적으로 오차항이 정규 분포(normal distribution)를 따른다고 가정한다. 이 가정은 yn 역시 정규 분포를 따르게 된다. 하지만 선택은 예 아니면 아니오, 0, 1 밖에 할 수 없는 변수이다. 0, 1 밖에 선택할 수 없는 모델에 일반적인 선형 모델을 선택하면 다음과 같은 그림이 나온다.
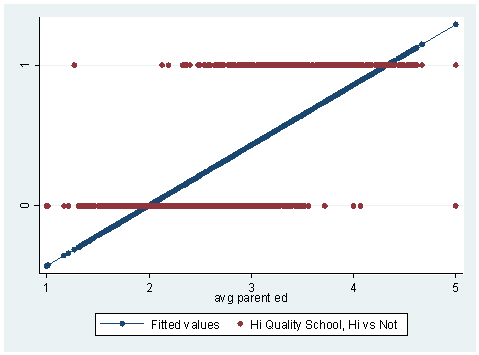
빨간색 점은 데이터고, 0과 1에 분포해있다. 파란색 점과 선은 선형 모델로, 모델이 데이터를 제대로 설명하지 못한다는 것을 알 수 있다. 즉, 이런 문제를 해결하기 위해서는 다른 가정을 쓰는 모델 = 로지스틱 회귀가 필요하다.
■ 오즈, 로짓과 로지스틱 회귀
로지스틱 회귀는 또 다른 말로 로짓 회귀(logit regression), 로짓 모델(logit model)이라고 부른다. 데이터의 레이블이 있는 지도 학습(Supervised learning) 중의 하나로, xi와 yi가 주어졌을 때 p(y|x)를 구한다.
로지스틱 회귀는 베르누이 분포를 따르는 1개의 동전 던지기 예시로 많이들 설명된다.
θ 가 [0, 1] 사이의 성공 확률이라고 할 때,
p(y|θ) = Ber(y|θ) = θ, y = 1
1-θ, y = 0
요 수식이 뭔 말인고 하면, 동전을 던져서 앞면이 나올 확률, 즉 성공 확률이 θ면, 확률 변수 y가 1 값을 갖고, 실패일 경우(1-θ)에는 확률 변수 y가 0값을 갖는다는 말을 수식으로 표현한 것이다. 베르누이 확률 변수의 기댓값과 분산은 다음과 같다.
E[Y] = 1*θ + 0 *(1-θ) = θ
Var[Y] = E[Y^2] - E[Y]^2 = θ - θ^2 = θ(1-θ)
로짓에 대해 알기 전에 오즈(Odds)의 개념을 먼저 알아야 한다. 오즈는 실패 비율 대비 성공 비율을 뜻하고, 수식으로는 다음과 같이 나타낸다.
odds(θ) = \frac{θ}{(1-θ)}로짓은 오즈에 로그를 씌운 log odds(θ)를 뜻하며, 로그 오즈 또는 로짓 함수(logit function)이라고도 부른다.
log odds(θ) = log( \frac{θ}{(1-θ)}) = logθ - log(1-θ)
이제 드디어 로지스틱 함수다. logit(θ)를 η (이타라고 부른다)라고 하면, θ의 성공 확률은 다음과 같다.
θ = σ(η) = \frac{1}{1+exp(-η)}이 식에서 σ(η) 을 로지스틱 함수라고 부른다. 흔히 시그모이드(Sigmoid)라고 부르는 함수이다. 이렇게 식을 변형 변형해가면서 로지스틱 함수를 만든 이유는, 로지스틱 함수가 비용 함수(cost function)을 0과 1사이로 만들어주기 때문이다.

오즈, 로짓과 다르게 로지스틱 함수는 우리가 확률을 해석하기 좋게 0과 1 사이의 값으로 만들어준다.
다시 우리의 마케팅 문제로 돌아가보자. 로지스틱 함수에서 쓰는, 우리가 이타(η)라고 명명한 녀석은 사실 선형 함수이다. 로지스틱 회귀가 logit(p(y=1 | x) = X와 선형관계가 있다고 가정을 하기 때문이다. 즉, 수식으로 표현하면 다음과 같다.
η = w_0 + w_1x_1 + w_2x_2 + ... + w_nx_n
우리한테 많이 익숙한 바로 선형 모델이다! 이타는 그저 가중치(w)와 속성(x)의 내적(inner product)인 셈이다. 로지스틱 회귀에서 w0을 bias term이라고 하는데, 보통 계산의 편의성을 위해 bias feature라고 부르는 x0에 1을 넣어서 w0값을 없애주곤 한다. 즉, x가 1, x1, x2 …, xn 으로 이뤄진 행렬이고, w가 w0, w1, w2, …, wn으로 이뤄진 행렬이라면 이 때의 이타는 두 행렬의 곱인 < w, x > 이다(내적을 수식으로 표현할 때 < w, x > 라고 쓰거나 wTx 라고 쓴다. 이 때 w와 x는 원소가 아니라 행렬임을 주의깊게 보자.)
bias feature가 들어가면 p(y|x, w) = Ber(y|σ(<w,x>)) 가 됨을 알 수 있다. <w,x>가 0보다 작으면 해당 성공 확률이 0.5보다 작게되므로 y값은 0이다. 반면에 <w,x>이 0보다 클 때 성공확률이 0.5보다 크게되고, y값은 1이 된다. 즉, 로지스틱 회귀에서의 결정 경계는 <w,x> = 0 일 때 나타난다.
■ 로지스틱 회귀 적용 예제
예제를 통해 로지스틱 회귀 문제를 살펴보자. 예를 들어 쿠팡에서 물건을 주문하는 사람의 효용 가치(utility)가 그 사람의 월소득(x1)과 성별(x2; 여자=0, 남자=1)에 의해 결정된다고 가정하자. 이 때 한 사람의 효용은 다음의 식을 따른다.
y_n = w_0 + w_nx_1 + w_nx_2+ ε_n
글의 초반부에서 설명했듯이 w0은 임의의 절편값이고, ε 는 관측할 수 없는 속성에 의한 오차값이다. 파라미터는 보통 알려진 값이거나 추정된다. 로지스틱 회귀에서는 MLE(최대우도법, Maximum Likelihood Estimation) 방법을 사용해서 파라미터값을 추정할 수 있다(MLE에 대한 자세한 설명은 다른 글에서 다루도록 하겠다).
예제에서는 이미 아래와 같이 파라미터가 알려졌다고 하자.
w0 = 0.5
w1 = -0.01
w2 = 1.1
월 소득이 400$인 남자가 쿠팡에서 물건을 주문할 확률을 로지스틱 함수를 이용해서 구해보자.
\frac{1}{1+exp(-η)} = \frac{1}{1+exp(-(0.5-0.01*400+1.1*1))} = \frac{1}{1+exp(2.4)} = 0.08주어진 모델에서 월 소득이 400$인 남자가 쿠팡에서 물건을 주문할 확률을 8%이다.
■ 로지스틱 회귀의 특징
- 로지스틱 회귀는 간단한 분류 모델(Discriminative Model)이다.
- 결과값을 확률로 주기 때문에 해석이 쉽다.
- 모델에 쉽게 적합 가능하다.
- 2개 이상의 분류기(classifier)에도 적용 가능하다 –> 소프트맥스 회귀는 간단한 분류 모델(Discriminative Model)이다.
- 비선형적인 결정 경계에도 적용 가능하다 –> 커널 로지스틱 함수로 가능