지난 글에서는 비선형 회귀 중 단조 증가라는 특별한 케이스일 때 적용하는 등회귀에 대해 알아보았다(등회귀 알아보기). 이번에는 X와 Y의 관계가 비선형이면서 X가 증가할 때 Y의 추세가 단조롭지 않은, non-monotonous 문제를 해결하는 방법에 대해 알아보자.
■ 비선형(non-linear) & 비단조(non-monotonous) 문제란?
우리가 지금 해결해야할 문제는 다음 그림과 같이 X와 Y의 관계가 비선형이고, X 값이 증감과 Y값의 증감에 어떤 패턴도 보이지 않는 경우를 말한다.

■ 다항 회귀(Polynomial Regression)로 변환
해결법 중 하나는 기존 선형 회귀에 새로운 속성(attribute)을 추가하는 것이다. 이를 통해 우리는 보다 복잡한 비선형 데이터 셋에 선형 회귀에서 사용하던 테크닉을 똑같이 사용할 수 있다. 새로 추가하는 속성은 원래 속성 X 값에 로그(log), 지수(exp), 제곱근(square root), 제곱(square) 등을 취하여 변환한 형태가 있다.
예를 들어 데이터 셋에 속성 X가 하나가 있을 때, 새로운 속성 X의 제곱(X2)을 추가하여 다항식으로 만들어준다. 이러한 속성은 파이썬 Scikit-learn의 라이브러리 중 PolynomialFeatures를 사용해서 쉽게 변환할 수 있다.
그 외에도 다음의 속성들을 새로 추가할 수 있다.
– 원래 속성 X
– 다항식 변환
y = β0 + β1x+ β2x2 + β3x3
– 교호작용(interaction) 속성으로의 변환:
x3 = x1 ㆍ x2
– 기저 확장(Basis Expansion)
다항 회귀는 속성과 계수의 관계가 선형이고, 다항식의 항은 속성이므로 종종 다중 선형 회귀(multivariate linear regression)의 특별한 케이스로 불리기도 한다.
■ 다항 회귀의 차수(degree)와 속성의 개수 관계
쉽게 생각해서 다항 회귀는 속성을 추가하여 선형 모델을 좀 더 복잡하게 표현할 수 있도록 확장한다고 볼 수 있다. 다항식의 “차수(degree)”에 따라 추가하는 속성의 개수가 달라진다.
- 속성: 1개(a), 차수: 3 —> a2, a3 추가
- 속성: 3개(a, b, c), 차수: 2 —> a2, b2, c2, ab, bc, ca 추가
- 속성: 3개(a, b, c), 차수: 3 —> a3, b3, c3, a2b, a2c, b2a, b2c, c2a, c2b, abc 추가
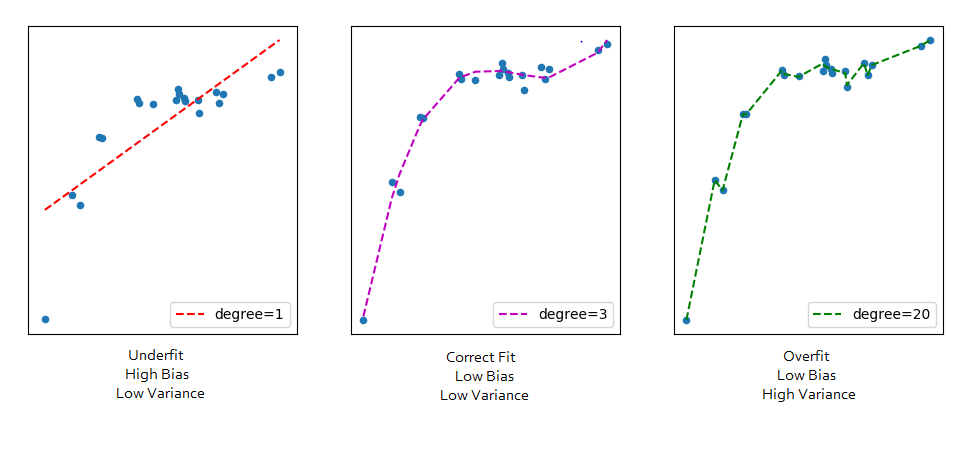
차수가 높아지면 새로운 속성도 기하급수적으로 늘어나 계산 시간이 오래걸리고 과적합(overfitting) 문제가 생긴다. 따라서 보통 2차식 또는 3차식을 사용한다. 아래는 차수가 늘어남에 따라 다항 회귀식이 어떻게 그려지는지 시각적으로 보여준다.
■ 다항 회귀의 평가
다항 회귀 역시 MSE(평균 제곱 오차, Mean Squared Error) 등으로 평가한다. MSE가 낮으면서도 과적합 문제가 없는 모델을 선택하는 것이 중요하겠다.